Table of Contents
- SCIENTIFIC CALCULATOR OPERATION GUIDE <EL-531TH Series>
- CONTENTS
- How to Operate
- Read Before Using
- Function and Key Operation
- ON/OFF, Entry Correction Keys
- Data Entry Keys
- Random
- Modify
- Basic Arithmetic Keys, Parentheses
- Percent
- Inverse, Square, Cube, xth Power of y, Square Root, Cube Root, xth Root of y
- 10 to the Power of x, Common Logarithm
- e to the Power of x, Natural Logarithm
- Factorials
- Permutations, Combinations
- Time Calculation
- Fractional Calculations
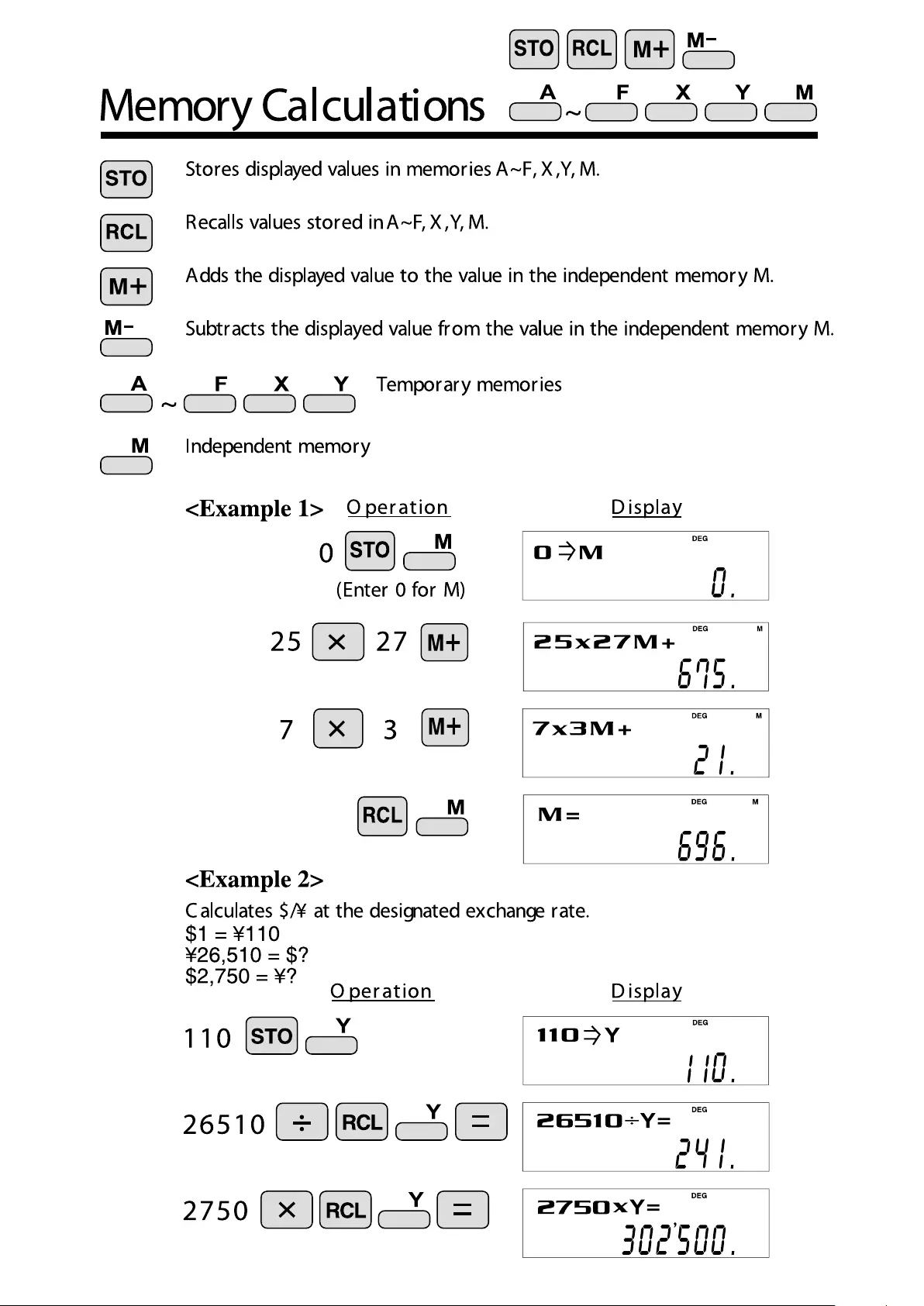
- Memory Calculations
- Last Answer Memory
- Trigonometric Functions
- Arc Trigonometric Functions
- Hyperbolic Functions
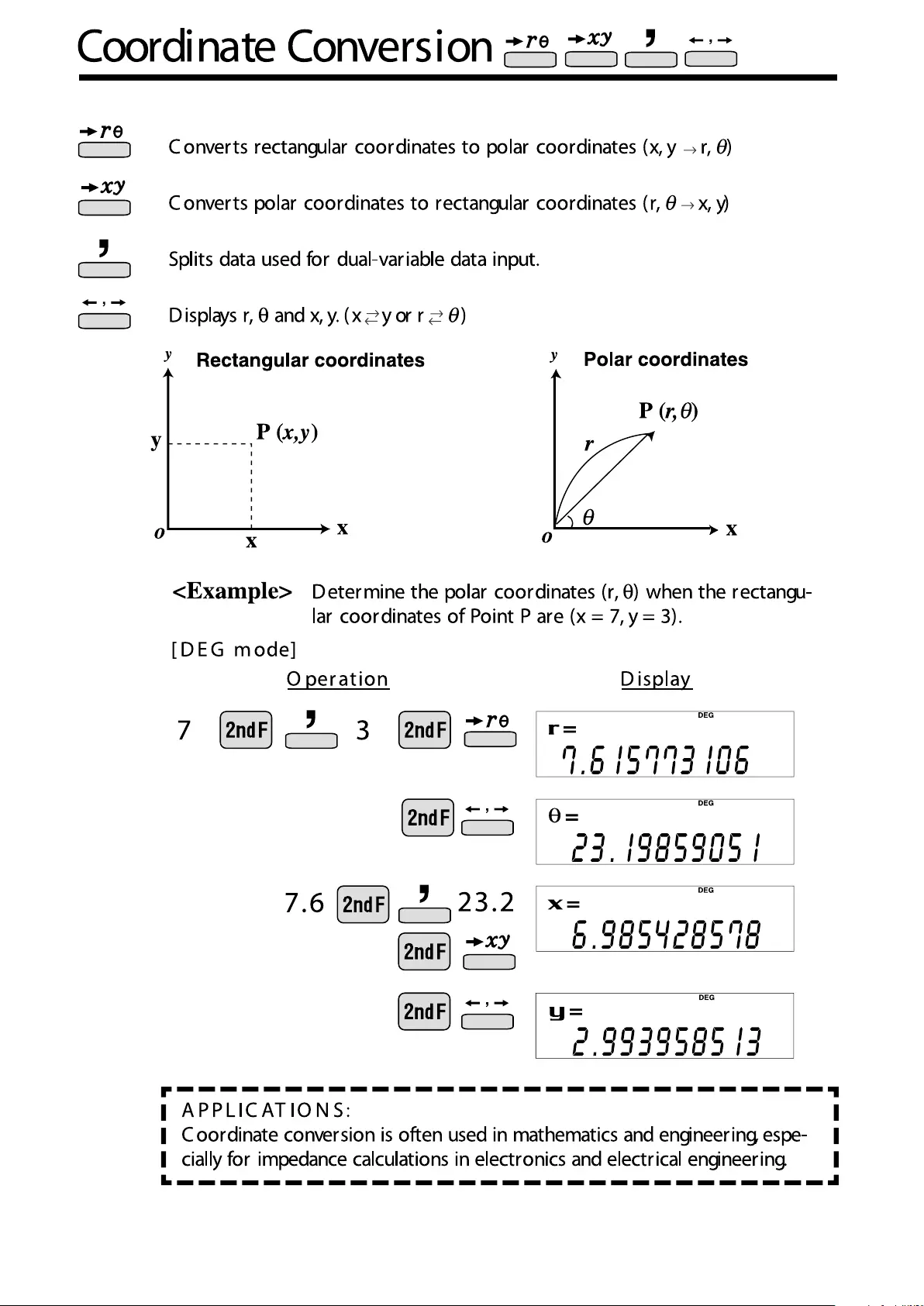
- Coordinate Conversion
- Binary, Pental, Octal, Decimal, and Hexadecimal Operations (N-Base)
- Statistics Function
Sharp EL-531TH User Manual
Displayed below is the user manual for EL-531TH by Sharp which is a product in the Calculators category. This manual has pages.
Related Manuals

1
< EL-531TH Series >

2
NEG
3
3
4
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
27
28
29
32
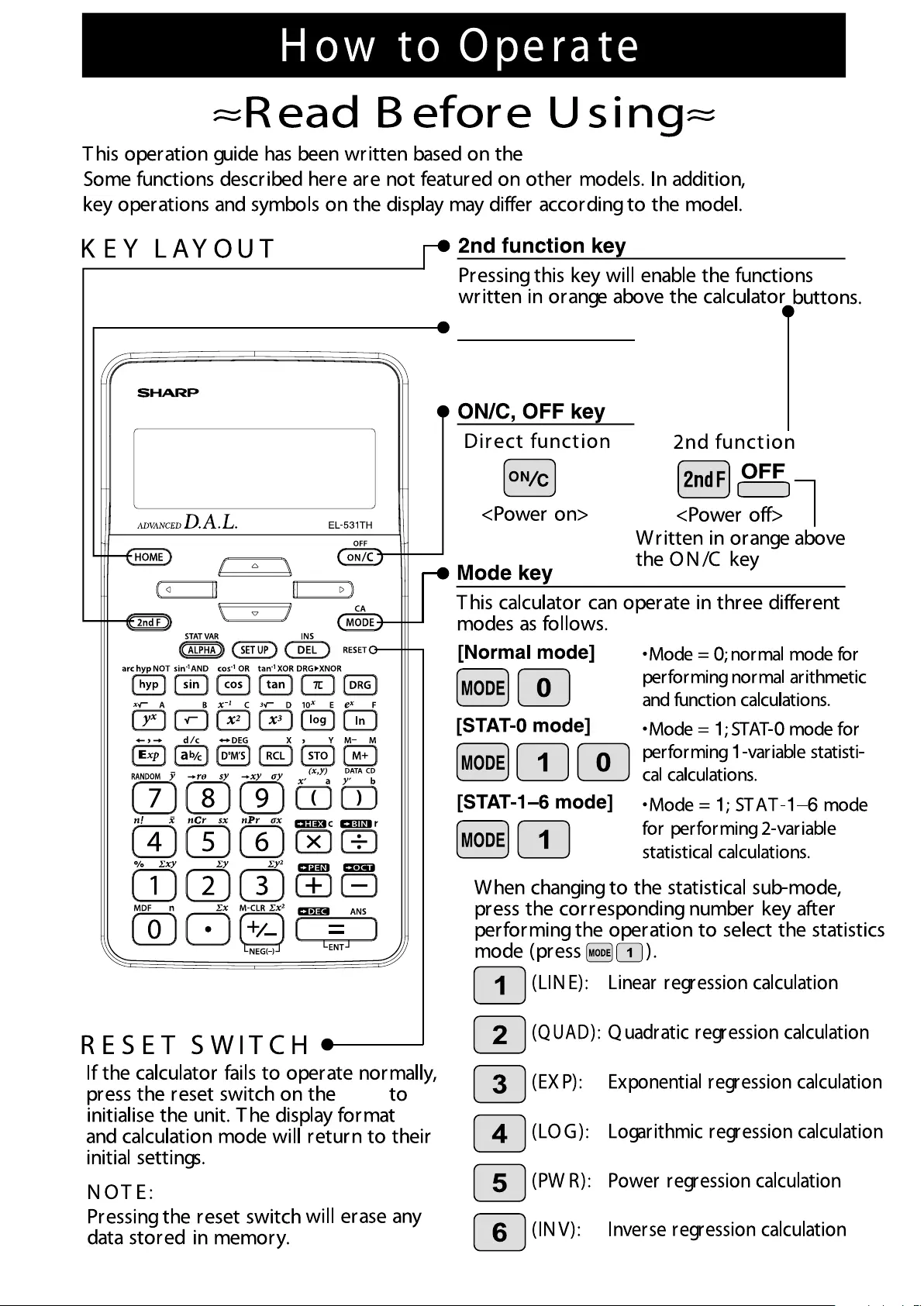
KEY LAYOUT
RESET SWITCH
DISPLAY PATTERN
DISPLAY FORMAT AND
DECIMAL SETTING FUNCTION
EXPONENT DISPLAY
ANGULAR UNIT
How to Operate
ON/OFF, Entry Correction Keys
Data Entry Keys
Basic Arithmetic Keys, Parentheses
Inverse, Square, Cube, xth Power of y,
Square Root, Cube Root, xth Root of y
10 to the Power of x, Common Logarithm
e to the Power of x, Natural Logarithm
Permutations, Combinations
Time Calculation
Fractional Calculations
Memory Calculations
Last Answer Memory
Trigonometric Functions
Arc Trigonometric Functions
Hyperbolic Functions
Coordinate Conversion
Binary, Pental, Octal, Decimal, and
Hexadecimal Operations (N-Base)
Statistics Function
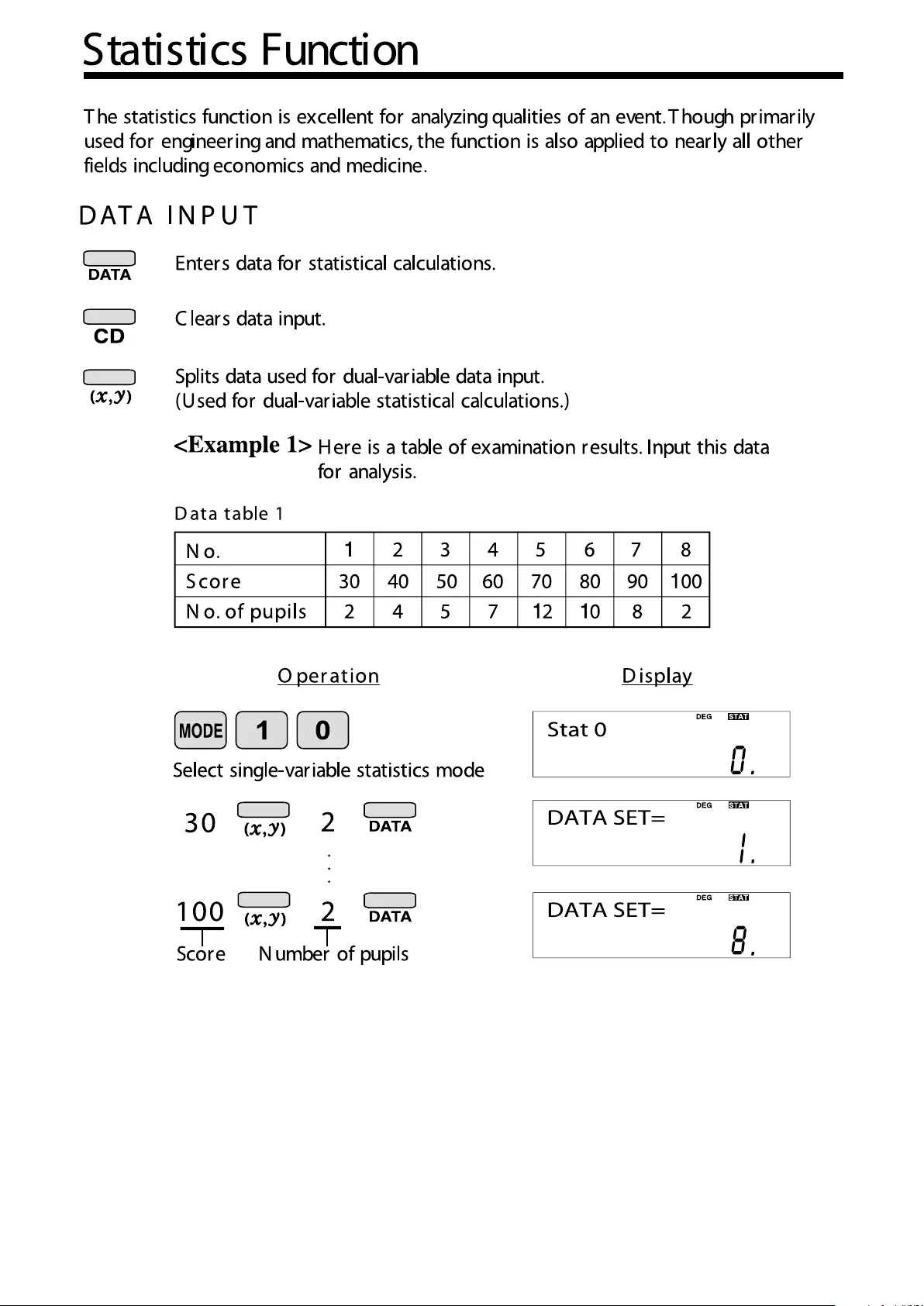
DATA INPUT
“ANS” KEYS FOR 1-VARIABLE STATISTICS
DATA CORRECTION
“ANS” KEYS FOR 2-VARIABLE STATISTICS
Random
Modify
Percent
Factorials
3
EL-531TH series.
front
HOME key
Pressing this key will return to
NORMAL mode.

4
FIX
5
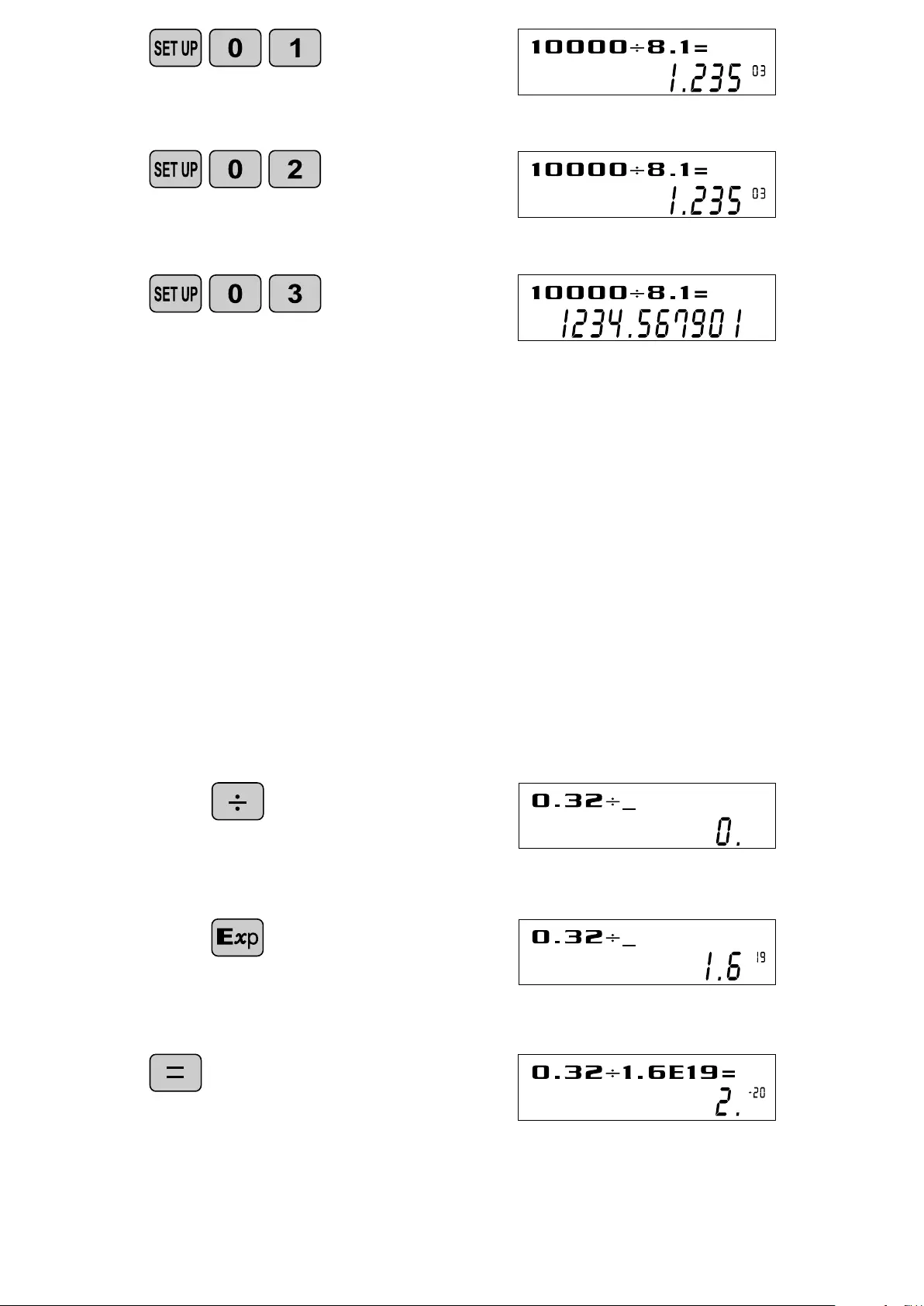
E X P O N E N T DI S P L AY
The distance from the earth to the sun is approx. 150,000,000 (1.5 x 108) km. Values
such as this with many zeros are often used in scientific calculations, but entering the
zeros one by one is a great deal of work and it’s easy to make mistakes.
In such a case, the numerical values are divided into mantissa and exponent portions,
displayed and calculated.
<Example> W hat is the number of electronics flowing in a conductor when
the electr ical char ge across a given cross-section is 0.32 cou-
lombs. (T he char ge on a single electron = 1.6 x 10-19 coulombs).
0.32 DEG
(SC I mode)
SCI DEG
X10
(EN G mode)
ENG DEG
X10
(nor mal mode)
DEG
191.6 DEG
X10
DEG
X10

6
7

8
NEG

9

10
Function to round calculation r esults.
Even after setting the number of decimal places on the display, the calculator per-
for ms calculations using a lar ger number of decimal places than that which appear s
on the display. By using this function, internal calculations will be perfor med using
only the displayed value.
APPLICATIONS:
Frequently used in scientific and technical fields, as well as business,
when perfor ming chained calculations.
<Example>
Rounded calculation (MDF)
FIX mode TAB = 1 (normal calculation)
5.0
0.6
0.6
5.4
59
9
5 9
9
Modify
(i nte r nally, 0.6)
(i nte r nally, 0.5555...)
(i nte r nally, 0.5555...)

11
Basic Arithmetic
Keys, Parentheses
Used to specify calculations in which cer tain oper ations have pr ecedence.
You can make addition and subtr action oper ations have precedence over
multiplication and division by enclosing them in parentheses.
T he four basic operators. Each is used in the same way as a standard
calculator :
+ (addition), – (subtr action), x (multiplication), and ÷ (division).
Finds the result in the same way as a standar d calculator.

12
13
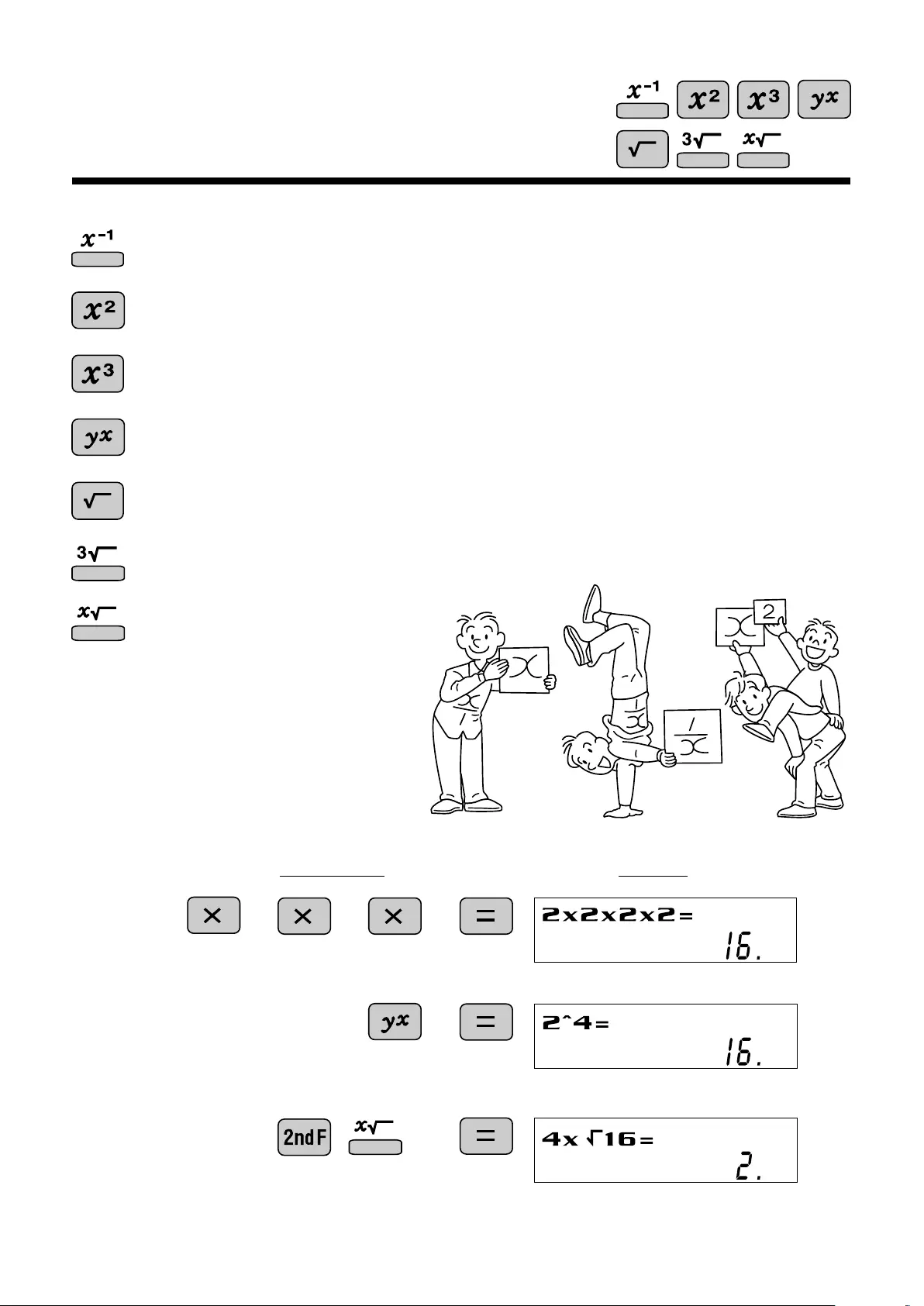
<Example>
C alculates the square root of the value.
C alculates the inverse of the value.
Squares the value.
C ubes the value.
C alculates the cube root of the value.
C alculates the xth root of y.
24
416
DEG
DEG
DEG
O peration Display
C alculates exponential values.
2 2 2 2
Inverse, Square, Cube,
xth Power of y, Square Root,
Cube R oot, xth R oot of y
14
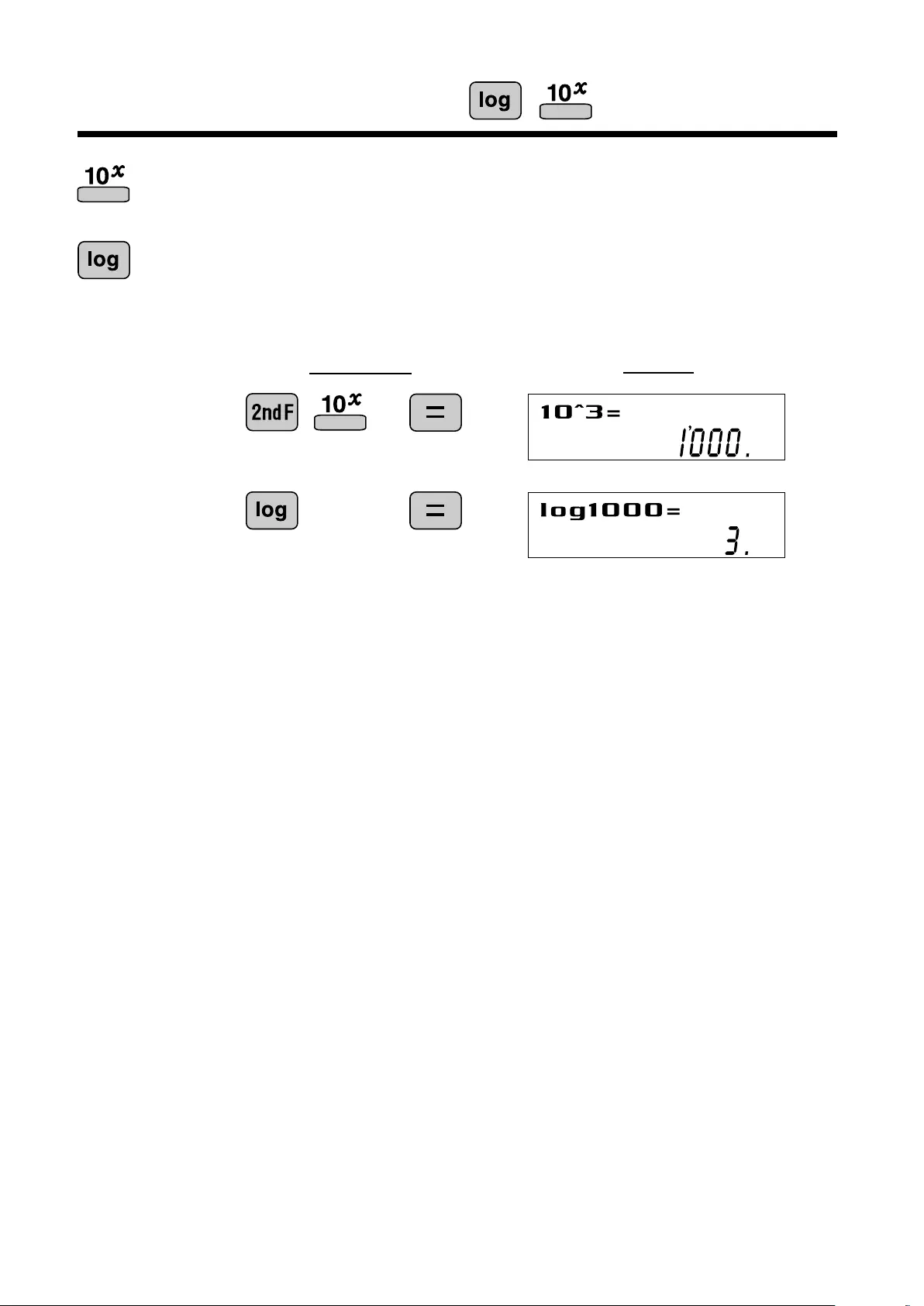
10 to the Power of x,
Common Logarithm
<Example>
C alculates the value of 10 r aised to the xth power.
C alculates logar ithm, the exponent of the power to which 10 must be
r aised to equal the given value.
1000
3
O peration Display
DEG
DEG

15
e to the Power of x,
Natural Logarithm
C alculates power s based on the constant e (2.718281828).
<Example>
5
10
O peration Display
DEG
DEG
C omputes the value of the natur al logar ithm, the exponent of the power
to which e must be raised to equal the given value.

16
Factorials
T he product of a given positive integer n multiplied by all the lesser positive
integers from 1 to n-1 is indicated by n! and called the factor ial of n.
APPLICATIONS:
Used in statistics and mathematics. In statistics, this function is used
in calculations involving combinations and permutations.
<Example>
c.f
n! = 1 x 2 x 3 x …xn
O peration Display
DEG
7
17
6 4
6 4
APPLICATIONS:
Used in statistics (pr obability calculations) and in simulation hypoth-
eses in fields such as medicine, pharmaceutics, and physics. Also,
can be used to deter mine the chances of winning in lotter ies.
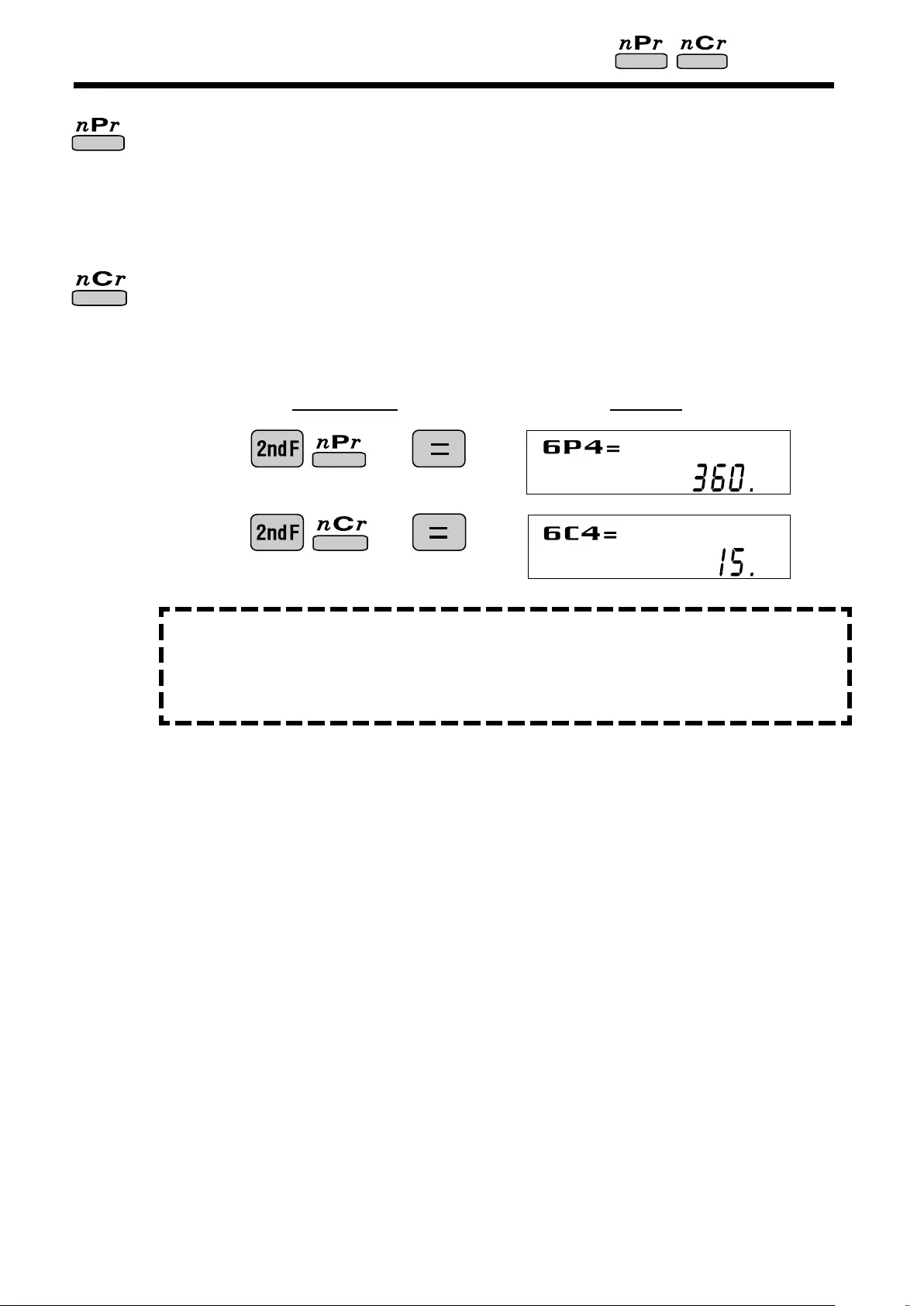
Permutations, Combinations
<Example>
T his function finds the number of different possible or der ings in selecting
r objects from a set of n objects. For example, there are six different
ways of ordering the letters ABC in groups of three letters—ABC , AC B,
BAC, BCA, CAB, and C BA.
T he calculation equation is 3P3 = 3 x 2 x 1 = 6 (ways).
T his function finds the number of ways of selecting r objects from a set of
n objects. For example, from the three letters ABC , there are three ways
we can extr act gr oups of two different letter s—AB, AC , and C B.
T he calculation equation is 3C2.
DEG
DEG
O peration Display

18

19
Fractional Calculations
Add 3 and , and convert to decimal notation.
<Example>
Inputs fractions and converts mutually between fractions and decimals.
C onverts between mixed numbers and improper fr actions.
312
57
C onvert to an improper fraction
Press once to return to the previous display
C onvert to decimal notation
Press once to return to the previous display
APPLICATIONS:
T her e is a wide variety of applications for this function because
fr actions ar e such a basic par t of mathematics. T his function is useful
for calculations involving electrical circuit resistance.
DEG
DEG
DEG
O peration Display
DEG
1
2
5
7
20

21
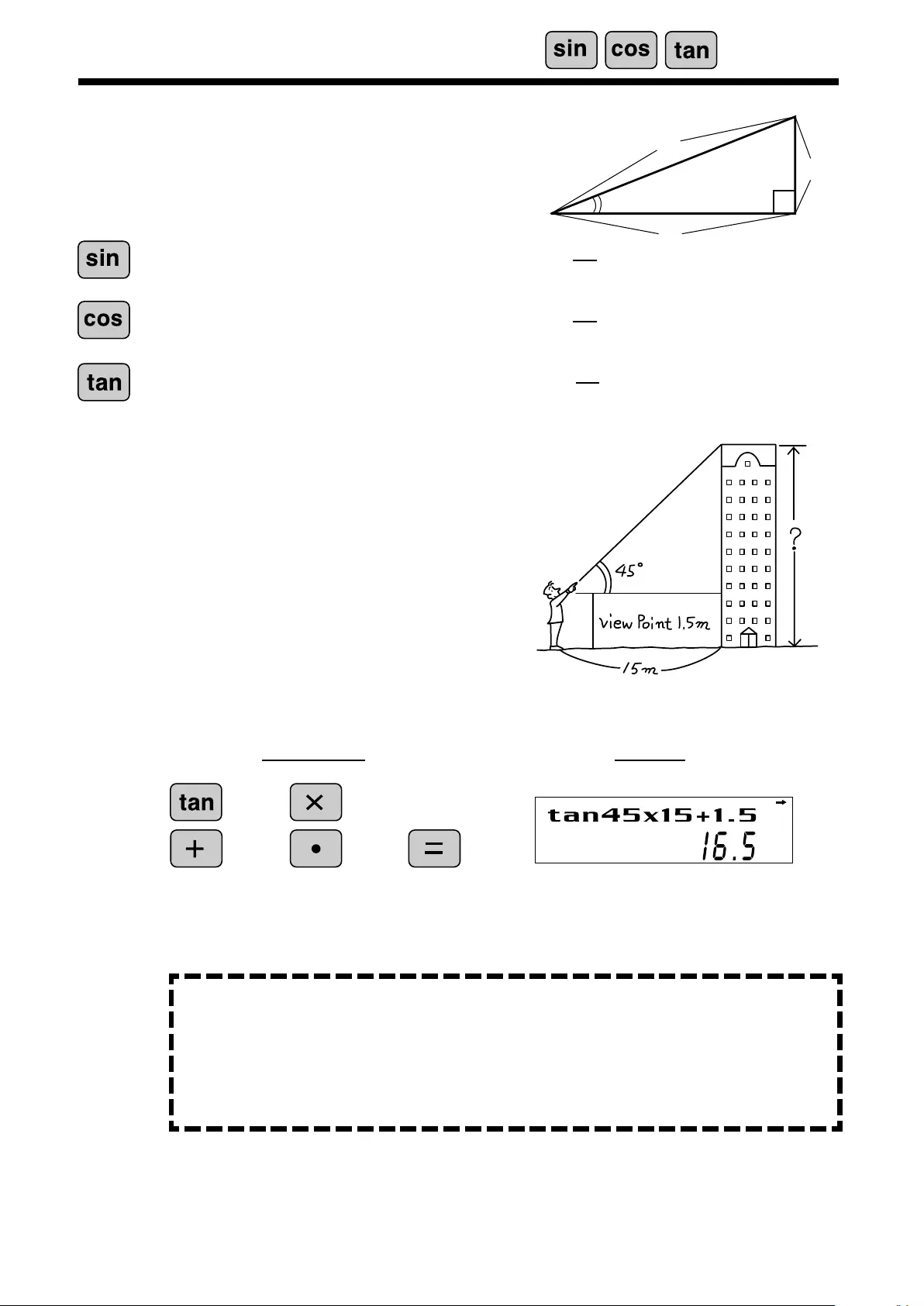
22
T he angle from a point 15 meters from
a building to the highest floor of the
building is 45°. How tall is the building?
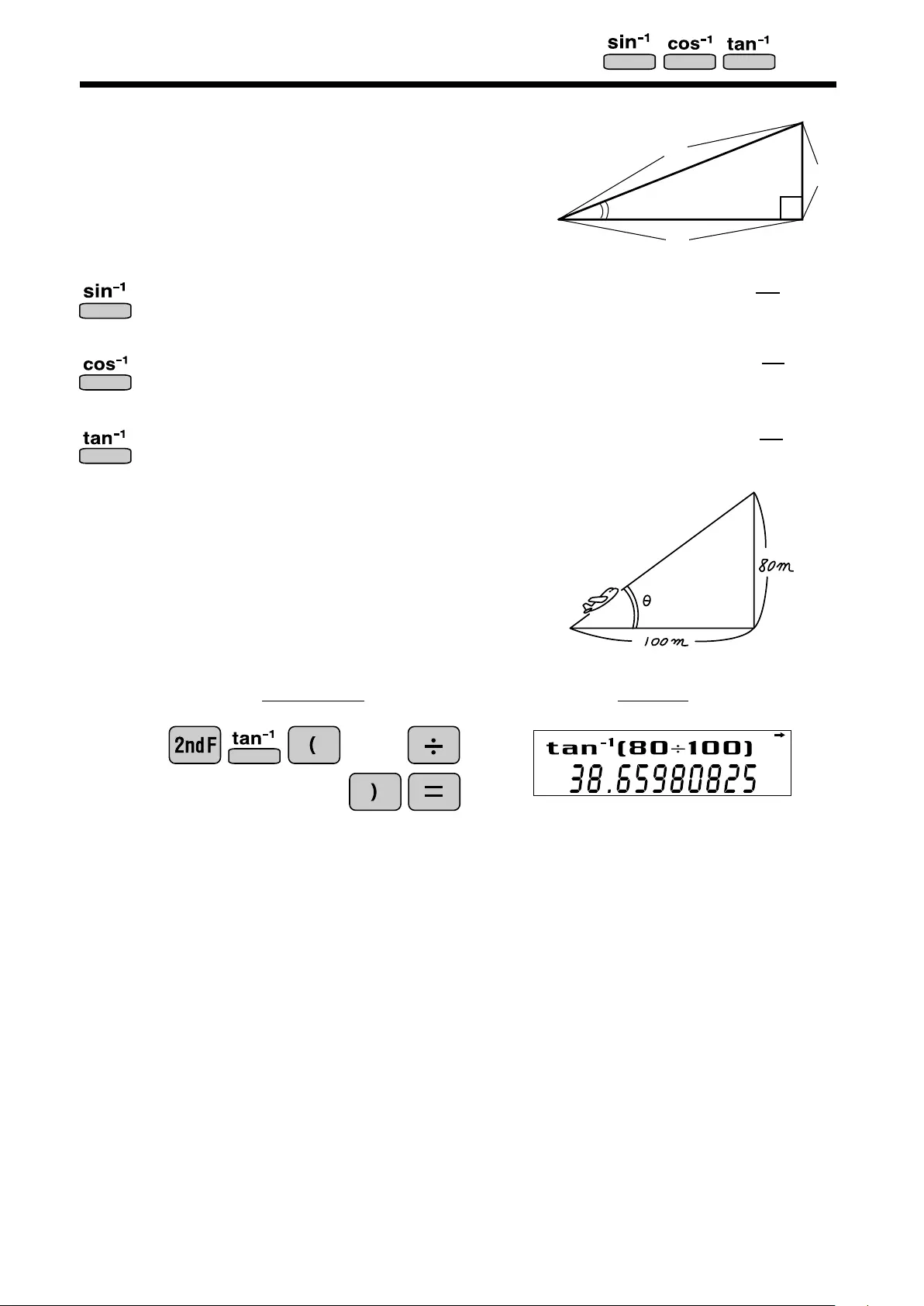
Trigonometric Functions
[DEG mode]
V
APPLICATIONS:
Tr igonometr ic functions are useful in mathematics and various engineer ing
calculations. T hey ar e often used in astronomical observations, civil engi-
neer ing and in calculations involving electrical circuits, as well as in calcula-
tions for physics such as parabolic motion and wave motion.
C alculates the sine of an angle.
C alculates the cosine of an angle.
C alculates the tangent of an angle.
<Example>
45 15
iew point
15
O peration Display
sin
θ
=b
a
tan
θ
=b
c
cos
θ
=c
a
a
c
b
θ
DEG
T rigonometric functions determine the ratio of three sides
of a r ight tr iangle. T he combinations of the thr ee sides ar e
sin, cos, and tan. T heir r elations ar e:
23
Arc trigonometr ic functions, the inverse of trigonomet-
r ic functions, are used to deter mine an angle from r atios
of a r ight tr iangle. T he combinations of the thr ee sides
are sin-1, cos-1, and tan-1. T heir relations are;
Arc Trigonometric Functions
[DEG mode]
(ar c sine) D eter mines an angle based on the r atio
b/a of two sides of a right tr iangle.
(ar c cosine) D eter mines an angle based on the r atio
c/a for two sides of a r ight tr iangle.
(arc tangent) D eter mines an angle based on the
r atio a/b for two sides of a right tr iangle.
<Example>
At what angle should an air plane climb in or der
to climb 80 meters in 100 meters?
80
100
O peration Display
θ
= sin-1 b
a
θ
= cos-1 c
a
θ
= tan-1 b
c
c
a
b
θ
DEG
24
Hyperbolic Functions
T he hyper bolic function is defined by using natur al exponents in tr igo-
nometr ic functions.
APPLICATIONS:
H yper bolic and arc hyper bolic functions are very useful in electrical
engineer ing and physics.
Arc hyper bolic functions are defined by using natur al logar ithms in tr igono-
metr ic functions.
25

26
27

28
C alculates the average value of the data (sample data x).
C alculates the standar d deviation for the data (sample data x).
C alculates the standar d deviation of a data population (sample data x).
D isplays the number of input data (sample data x).
C alculates the sum of the data (sample data x).
C alculates the sum of the data (sample data x) r aised to the second power .
Let’s check the r esults based on the previous data.
69 (average value)
17.75686128 (standard deviation)
17.57839583 (standard deviation of the population)
50 (total count of data)
3450 (total)
NOTE:
1.Sample data refer s to data selected r andomly from the population.
2. Standard deviation of samples is determined by the sample data
shift from an aver age value.
3. Standar d deviation for the population is standard deviation when
the sample data is deemed a population (full data).
“ANS” K EYS FOR 1-VARIABLE STATISTICS
29
DATA CORRECTION
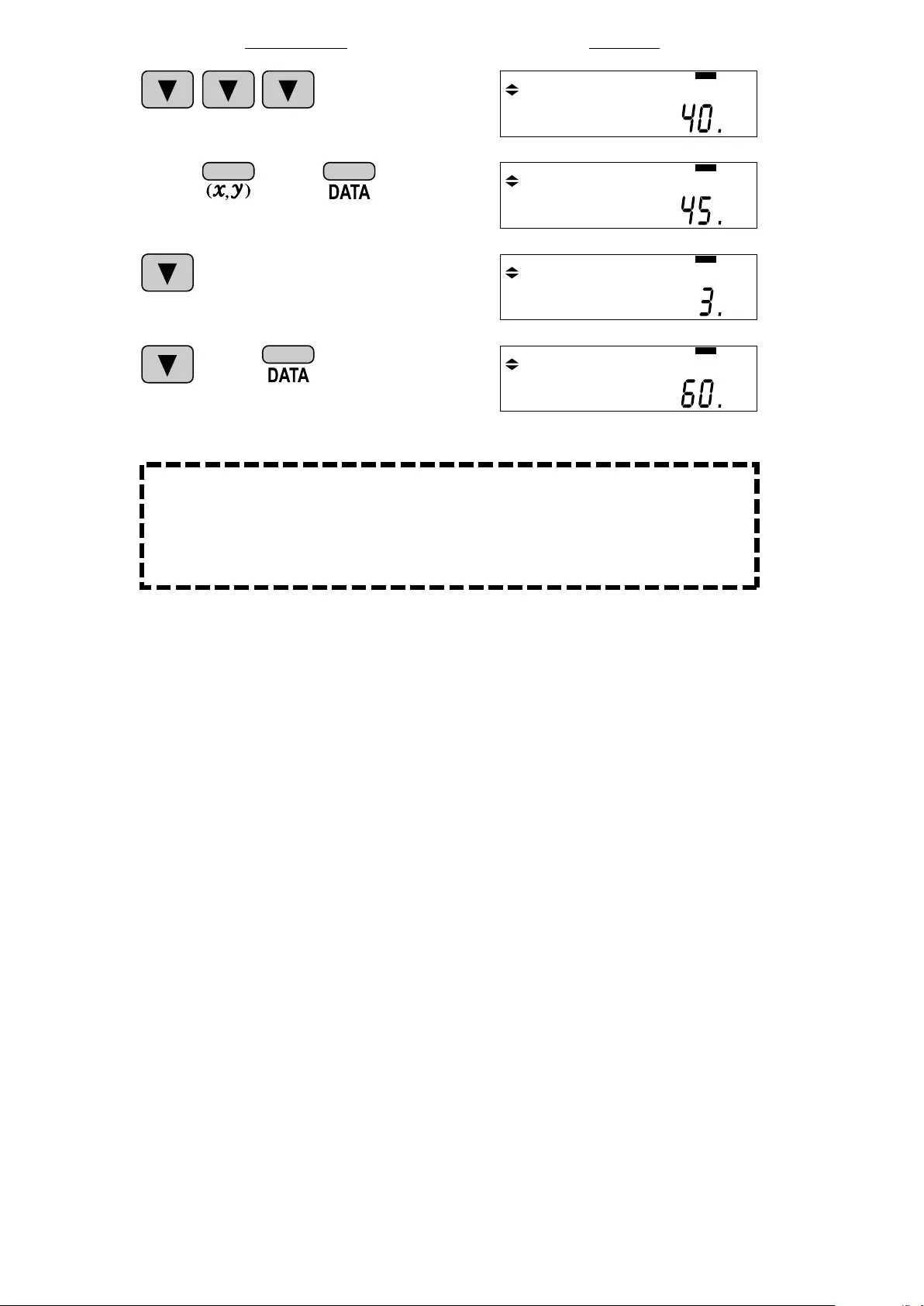
<Example 2>
30
40
50
2
O peration Display
Select single-variable statistics mode
DEG STAT
Stat 0
DEG STAT
DATA SET=
Correction after pressing :
C orrection prior to pressing immediately after a data entry: Delete incorrect
data with , then enter the cor r ect data.
Use to display the data previously entered.
Pr ess to display data items in ascending (oldest first) or der . T o
reverse the display order to descending (latest first), press the key.
Each item is displayed with 'X n=', 'Y n=', or 'N n=' (n is the sequential
number of the data set).
D isplay the data item to modify, input the cor r ect value, then pr ess .
Using , you can cor r ect the values of the data set all at once.
• �W hen or
appears, more data items can be browsed by pressing �
� or .
•�To delete a data set, display an item of the data set to delete, then ��
� press . T he data set will be deleted.
• �T o add a new data set, pr ess and input the values, then pr ess .
Data table 2
X: 30, 40, 40, 50
X: 30, 45, 45, 45, 60
DEG STAT
DATA SET=
DEG STAT
DATA SET=
30
APPLICAT IONS:
Single-variable statistical calculations ar e used in a broad r ange of fields,
including engineering, business, and economics. T hey are most often applied to
analysis in atmospher ic observations and physics experiments, as well as for
quality control in factories.
45
60
3
O peration Display
DEG STAT
X2=
DEG STAT
X2=
DEG STAT
N2=
DEG STAT
X3=
31
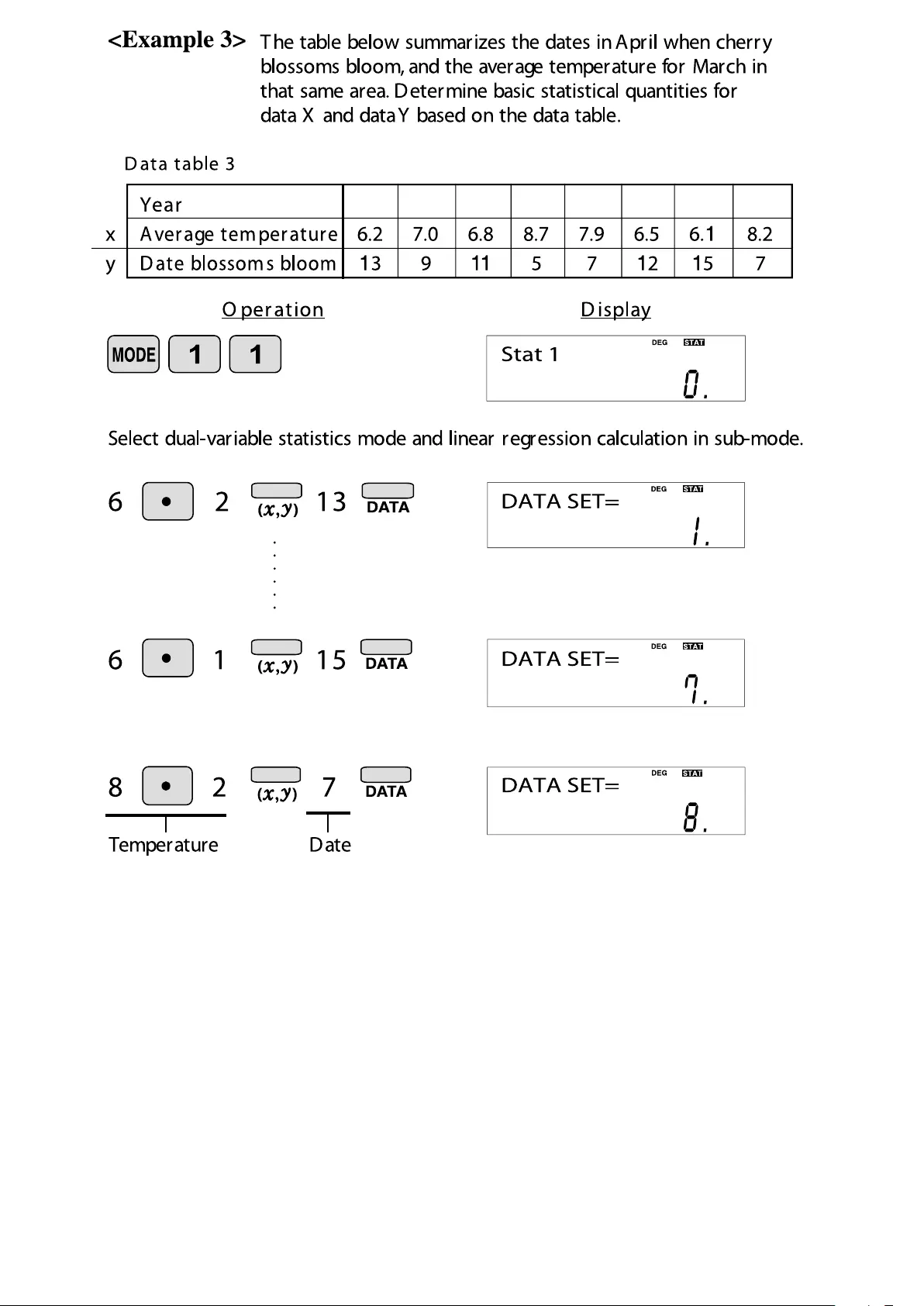
2010 2011 2012 2013 2014 2015 2016 2017

32
7.175 (Aver age for data x)
0.973579551(Standar d deviation for data x)
0.91070028 (Standar d deviation of the population for data x)
9.875 (Aver age for data y)
3.440826313(Standar d deviation for data y)
3.218598297 (Standar d deviation of the population for data y)
8 (Total count of data)
57.4 (Sum of data x)
418.48 (Sum of data x raised to the second power )
544.1(Sum of the pr oduct of data x and data y)
79 (Sum of data y)
863 (Sum of data y r aised to the second power )
Let’ s check the results based on the previous data.
C alculates the sum of the product for sample data x and sample data y.
C alculates the sum of the data (sample data y).
C alculates the sum of the data (sample data y) r aised to the second power .
C alculates the aver age value of the data (sample data y).
In addition to the 1-variable statistic keys, the followi ng k eys have been added for calcu-
lating 2-variable statistics.
C alculates the standard deviation of a data population (sample data y).
C alculates the standard deviation for the data (sample data y).
NOTE:
T he codes for basic statistical quantities of sample data x and their meanings
are the same as those for single-variable statistical calculations.
“ANS” K EYS FOR 2-VARIABLE STATISTICS

33
SHARP CORPORATION (SEP. 2017)
17JSC95E1